[ML] PCA 主成份分析
在上一篇的文章中,檸檬爸首先介紹如何使用 Python 與 Numpy 函式庫將想要分析的圖片載入多維的空間中,接下來就是需要開始分析這些圖片,假設一開始並不知道這些圖片的標籤的時候,我們沒有辦法執行分類的訓練。本篇想要介紹一下 Principle Component Analysis, PCA 主成份分析這一個方法背後的數學理論與物理意義,參考的是台大資工系林軒田教授的講義,在林教授的講解過程中,PCA 其實是 Auto-Encoder 中的一個線性特例,如果從 Auto-Encoder 的角度來看 PCA 的話可以更加了解 PCA 主成份分析的物理意義!
一般情況的 Auto-Encoder
可以描述成以下的數學式,輸入是維度為 (1) 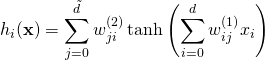
線性的 Auto-Encoder
線性的情況則可以描述成以下的數學式,輸入是維度為 (2) 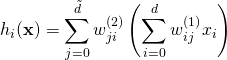
(3) ![]()
物理意義
首先我們利用 eigen-decompose 的技術將 (4) ![]()
所以線性 Auto-Encoder 的物理意義就是:
- 先利用一個 orthonormal 的基礎向量集合 V 將 x 向量轉置到另外一個向量空間 (Vector Space)
- 將一部分維度放大縮小,另外一部分維度設成 0
- 再利用同一組基礎向量集合將處理過後的向量轉回原本的向量空間
(5) ![]()
Problem Formulation 問題表述
有了以上對 Auto-Encoder 的描述,我們可以架構我們的問題為:找出一個最佳化的矩陣 (6) 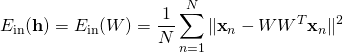
求解 W
以下我們 go through 一遍講義中的線性代數證明,也就是求解以下的最佳化問題:
(7) 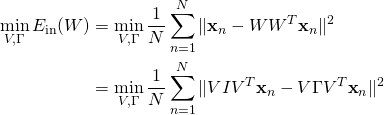
因為使用 orthonormal 的向量集合轉置到另外一個向量空間並不會影響長度,所以我們將問題簡化,
(8) 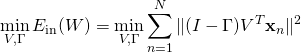
(9) 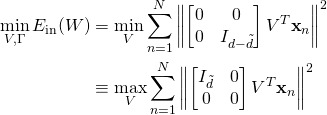
(10) 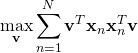
PCA 與 Auto-Encoder 的差異
其實 PCA 與 Auto-Encoder 在處理的問題還是有一點差異的,Auto-Encoder 是在處理最大化長度的問題,而 PCA 則是在處理最大化變異數的問題,但是其實兩個問題的本質是一樣的。
(11) 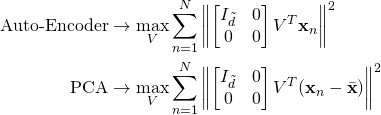
PCA 在 Clustering 的應用實例
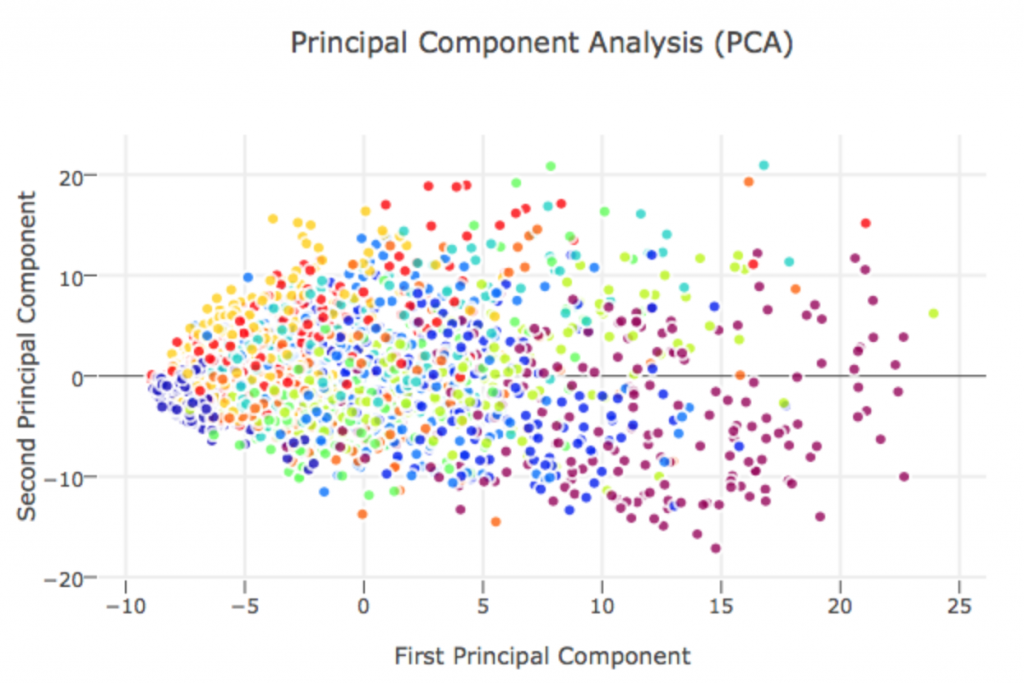
在以下連結中,作者使用 scikit-Learn 中的 PCA 主成份分析工具分析 MNIST 的圖片:
原本資料維度為 28 * 28 = 784 維,本篇作者展示將資料降維成 40 維一樣可以保持資料之間的差異性保持住,這邊值得一提的作者執行 PCA 之前有用
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)先將資料去平均值與正規化,其實就是式子 (11) 在做的事情,取最大變異的兩個維度,可以得到以下的結果,結果顯示利用 PCA 降成兩個維度在做機器學習的效果可能部會太好,這邊可能要考慮使用一些非線性的分類方法,例如 t-SNE 等等!
One thought on “[ML] PCA 主成份分析”