[統計] Chi-Square Test 卡方檢定

Posted on by
Post Views: 5,688

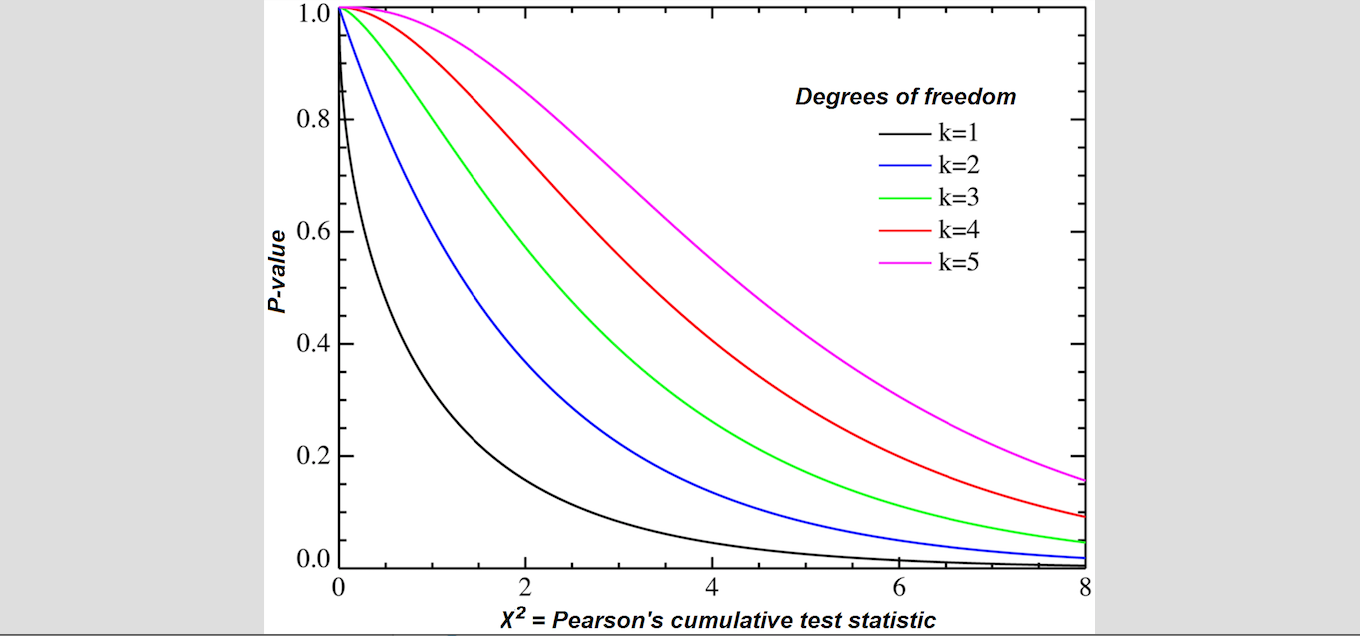
Chi-Square Test 卡方檢定或稱為 Chi-Squared Goodness of Fit Test 主要是透過一個樣本取樣來檢測我們是否有足夠的信心去使用 Multinomial 分佈描述這個取樣目標的隨機行為？本篇的數學推導主要參考 Michael J. Evans and Jeffrey S.Rosenthal 著作的 Probability and Statistic, The Science of Uncertainty 一書。

目標變數假設總共有 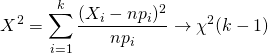k 個分類，假設做取樣的結果在 k 個分類中各自共有 X=(X_1,\cdots,X_k) 的樣本數，且總共取樣樣本數為 \sum_kX_k = n，如果 (X_1,\cdots,X_k) \sim Multinomial(n, p_1, \cdots, p_k) 的話，那麼 X^2 會呈現自由度 k-1 的 \chi^2 分佈。

(1)   \begin{equation*} X^2 = \sum^{k}_{i=1}\frac{(X_i-np_i)^2}{np_i}\rightarrow\chi^2(k-1) \end{equation*}

利用數學式 (1) 的特性，我們就可以計算出取樣的樣本位於整個分佈的哪一個位置，以此我們就可以利用統計的特性來推翻我們想要檢定的假設與否！以下我們想要紀錄數學的推導過程！推導參考的是由 A. W. van der Vaart, 著作的 Asymptotic Statistics 一書中的 17.2 定理：

首先我們將 X 向量拆解成 Y_1, \cdots, Y_n 個單位向量，且 \sum^n_{i=1}Y_i = X，則關於 Y_i 這一個隨機向量的統計特性的描述可以用以下表示：

(2)   \begin{equation*} \text{E}[Y_i] = (p_1,\cdots,p_k), \text{Cov}[Y_i]=\begin{pmatrix} p_1(1-p_1) & -p_1p_2 & \cdots & -p_1p_k\\ -p_2p_1 & p_2(1-p_2) & \cdots & -p_2p_k\\ \vdots& \vdots & & \vdots\\ -p_kp_1 & -p_kp_2 & \cdots & -p_k(1-p_k) \end{pmatrix} \end{equation*}

根據多變數中央極限定理 (multivariate central limit theorem)，則 X_n 可以由 Y_i 的統計特性描述：

(3)   \begin{align*} \left(\frac{X_{n,i} - np_i}{\sqrt{np_i}},\cdots\right) &\sim N_k(0, \text{Cov}[Y_i])\\ \left(\frac{X_{n,i} - np_i}{\sqrt{np_i}},\cdots\right) &\sim N_k\left(0,\begin{pmatrix} (1-p_1) & -\sqrt{p_1p_2} & \cdots & -\sqrt{p_1p_k}\\ -\sqrt{p_2p_1} & (1-p_2) & \cdots & -\sqrt{p_2p_k}\\ \vdots& \vdots & & \vdots\\ -\sqrt{p_kp_1} & -\sqrt{p_kp_2} & \cdots & -(1-p_k) \end{pmatrix}\right)\\ \left(\frac{X_{n,i} - np_i}{\sqrt{np_i}},\cdots\right) &\sim N_k(0,I-\sqrt{p}\sqrt{p}^T) \end{align*}

套用以下的定理一，我們可以推導

代入 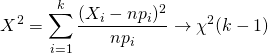\Sigma = I-\sqrt{p}\sqrt{p}^T，由於 \sum_ip_i = 1，所以矩陣中有一行可以是其他的線性組合，所以 rank < k，所以 \lambda_i 中有一個是 0 ，其他 k-1 都是 1，所以

(4)   \begin{equation*} X^2 = \sum^{k}_{i=1}\frac{(X_i-np_i)^2}{np_i}\rightarrow\chi^2(k-1) \end{equation*}

定理一：
如果 X 向量是 N_k(0,\Sigma) 的高斯分佈的話，那麼 \|X\|^2 的分佈與 \sum^{k}_{i=1}\lambda_i Z_i 一致，其中 \lambda_1,\cdots,\lambda_k 是 \Sigma 矩陣的 eigenvalues，而 Z_1, \cdots, Z_k 則是 i.i.d 的 N(0,1) 的高斯分佈。
定理一證明：
假設存在一個正交的矩陣 O，也就是說 O^TO=OO^T=I，可以使得 O\SigmaO^T = \text{diag}(\lambda_i)，那麼 OX 向量就會呈現 N_k(0, \text{diag}(\lambda_i)) 這一個 k 維的高斯多變數分佈，於是乎 \|X\|^2=\|OX\|^2=\sum_i\lambda_i Z^2_i。

以下分享一個 Chi-Square Test 的實作範例，可以透過取樣的數據去檢測我們的樣本是否可以用 Multinomial 的分佈來描述？

備註：

如果去探討兩個 Chi-Square Test 的 Multinomial 分佈是否有關係就是 Fisher Exact Test 在處理的進階問題。