[統計] 為什麼樣本標準差要除以 n-1 ?

Posted on by
Post Views: 4,750

本篇想要簡單的紀錄並且回答一個學習統計的人會遇到的問題，其實有不少統計的老師有討論過這個問題例如連結，但是並不是經過一個比較嚴謹的數學推導，本篇取材的來源是由 Michael J. Evans and Jeffrey S.Rosenthal 著作的 Probability and Statistic, The Science of Uncertainty 一書，點擊即可以下載。

假設 n 是取樣的樣本數，X_i 是 i.i.d 取樣值，而且呈現高斯分佈，我們用 N(\mu,\sigma^2) 表示，i = {1,...,n}。此時我們可以很快速的計算樣本的平均值 \bar{X} 為

(1)   \begin{equation*} \bar{X} = \frac{X_1+...+X_n}{n} \end{equation*}

根據高斯函數的特性我們知道平均值呈現的分佈是 \bar{X}\sim N(\mu,\frac{\sigma^2}{n})，所以此時我們可以利用樣本的平均值來做預測母體的平均值！但是此時我們要怎麼知道母體的變異數 \sigma^2 呢？我們可以使用樣本的變異數 \hat{\sigma}^2 來做估計嗎？

(2)   \begin{equation*} \hat{\sigma}^2=\frac{\sum^n_{i=1}(X_i-\bar{X})^2}{n} \end{equation*}

此時我們必需要先問自己一個問題，這個 \hat{\sigma}^2 的分佈長成什麼樣子？經過推導我們得知樣本變異數的分佈呈現 Chi-Square 自由度 n-1 的分佈 \hat{\sigma}^2\sim \frac{\sigma^2}{n}\chi^2(n-1)。接下來我們利用 \chi^2 的平均值特性

(3)   \begin{equation*} E[\chi^2(n-1)]=n-1 \end{equation*}

可以推演出樣本變異數的平均值會與母體變異數有以下的關係：

(4)   \begin{equation*} E[\hat{\sigma}^2] = \frac{n-1}{n}\sigma^2 \end{equation*}

所以套用第 (2) 式，我們可以得到

(5)   \begin{align*} \sigma^2 = \frac{n}{n-1}E[\hat{\sigma}^2] &= \frac{n}{n-1}E \left [\frac{\sum^{n}_{i=1}(X_i-\bar{X})^2}{n} \right] \\ &= \frac{1}{n-1}E \left [\sum^{n}_{i=1}(X_i-\bar{X})^2 \right ] \end{align*}

在統計的學術範疇裡面樣本的變異量在計算的時候通常是使用以下的公式：

(6)   \begin{equation*} \frac{1}{n-1}\sum^{n}_{i=1}(X_i-\bar{X})^2 \end{equation*}

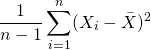
主要是因為在取樣的時候，我們無法知道究竟樣本變異數的平均值是多少，所以最好估計母體變異數的方法就是直接計算樣本變異數並且經過貝索校準 (Bessel Correction)。

證明：關於 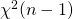\chi^2(n-1) 分佈的推導，可以參考書中的 Proof of Theorem 4.6.6。

在開始證明之前我們需要先準備好 Chi-Square 的定義與另外一的定理作為基礎：

定義一：
我們先說明 chi-square distribution with n degrees of freedom 或是 \chi^2(n) 或是 chi-squared(n)的定義是以下 Z 的機率分佈：

(7)   \begin{equation*} Z = X^2_1 + X^2_2 + ... + X^2_n \end{equation*}

這邊假設取樣的值 X_1,...,X_n 是 i.i.d 而且是 N(0,1)。
定理一：(高斯分佈的線性組合也是高斯分佈)
假設 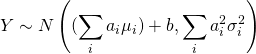X_i \sim N(\mu_i, \sigma^2_i) 且 i=1,2,...,n，他們之間互為獨立的隨機變數，假設一隨機變數 Y = \sum_i a_iX_i + b，其中 {a_i} 與 b 都是常數，則

(8)   \begin{equation*} Y \sim N\left ( (\sum_i a_i\mu_i)+b, \sum_i a^2_i\sigma^2_i \right ) \end{equation*}

使用了以上的兩個基礎之後：

則很神奇的 \frac{n}{\sigma^2}\hat{\sigma}^2 可以拆解成以下 n-1 的獨立的隨機變數而且他們都是 N(0,1)

(9)   \begin{align*} \frac{n}{\sigma^2}\hat{\sigma}^2 &= \sum^{n}_{i=1}\left (\frac{X_i - \bar{X}}{\sigma^2} \right )^2 \\ &= \left(\frac{X_1 -X_2}{\sigma\sqrt{2}} \right)^2 + \left(\frac{X_1+X_2-2X_3}{\sigma\sqrt{2\times3}} \right)^2 \\&+ ... + \left(\frac{X_1+...+X_{n-1}-(n-1)X_n}{\sigma\sqrt{(n-1)\times n}} \right)^2 \\ &= Y_1 + Y_2 + ... + Y_{n-1} \\ &\sim \chi^2(n-1) \end{align*}

根據定理一，Y_j\sim N(0,1)，j=1,...,n-1。