[統計] Fisher Exact Test
Fisher Exact Test 是一個檢驗兩個變數是否相關的方法?在基因大數據的領域裡面算是很常見的方法之一,詳細可以參考連結,由於在研讀 Fisher Exact Test 的時候,我們發現大部分網路上可以找到的訊息例如連結一,連結二都只有直接展示計算的結果但是沒有推導所以我們很難真正理解這些數學式背後的意義,本篇的推導參考 Michael J. Evans and Jeffrey S.Rosenthal 著作的 Probability and Statistic, The Science of Uncertainty 一書。
使用 Fisher Exact Test 的方法
以下我們展示 Fisher Exact Test 是怎麼驗證兩個隨機變數 (1) ![]()
(2) 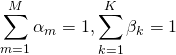
(3) ![]()
(4) 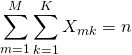
(5) 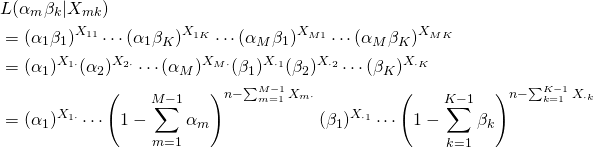
(6) ![]()
(7) 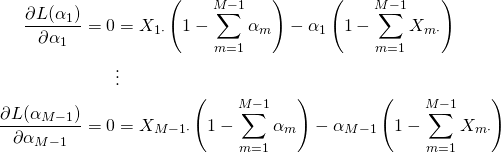
(8) ![]()
Fisher Exact Test 假設檢定的精神是觀察取樣的 P value 是否足夠低,足夠去推翻我們做的獨立性假設,
在一個 (9) 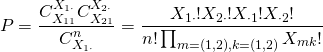
(10) ![]()
要判斷 P 值是否小於一個閾值還需要把所有小於這個 P 值的所有情況加總起來,在 2×2 以外的情況比較難做計算,因為很難窮舉,連結文章在介紹這個做法!